Grid Unit

Overview

The Grid unit has four subunits: GridMain is responsible for maintaining the Eulerian grid used to discretize the spatial dimensions of a simulation; GridParticles manages the data movement of Lagrangian quantities represented by particles; GridBoundaryConditions handles the application of boundary conditions at the physical boundaries of the domain; and GridSolvers includes implementations of solvers that need to know the details of the mesh and may be used by multiple physics solvers. In the Eulerian grid, discretization is achieved by dividing the computational domain into one or more sub-domains or blocks and using these blocks as the primary computational entity visible to the physics units. A block contains a number of computational cells (nxb in the \(x\)-direction, nyb in the \(y\)-direction, and nzb in the \(z\)-direction). A perimeter of guardcells of width nguard cells in each coordinate direction, surrounds each block of local data, providing it with data from the neighboring blocks or with boundary conditions, as shown in . Since the majority of physics solvers used in Flash-X are explicit, a block with its surrounding guard cells becomes a self-contained computational domain. Thus the physics units see and operate on only one block at a time, and this abstraction is reflected in their design.

Therefore any mesh package that can present a self contained block as a computational domain to a client unit can be used with Flash-X. However, such interchangeability of grid packages also requires a careful design of the Grid API to make the underlying management of the discretized grid completely transparent to outside units. The data structures for physical variables, the spatial coordinates, and the management of the grid are kept private to the Grid unit, and client units can access them only through accessor functions. This strict protocol for data management along with the use of blocks as computational entities enables Flash-X to abstract the grid from physics solvers and facilitates the ability of Flash-X to use multiple mesh packages.

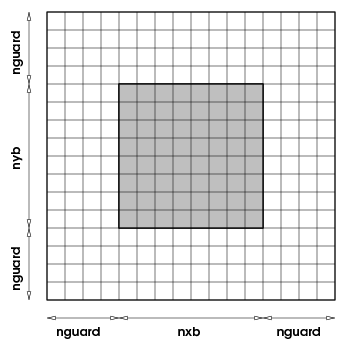
One block with its surrounding halo of guardcells

Any unit in the code can retrieve all or part of a block of data from the Grid unit along with the coordinates of corresponding cells; it can then use this information for internal computations, and finally return the modified data to the Grid unit. The Grid unit also manages the parallelization of Flash-X. It consists of a suite of subroutines which handle distribution of work to processors and guard cell filling. When using an adaptive mesh, the Grid unit is also responsible for refinement/derefinement and conservation of flux across block boundaries.

Flash-X can interchangeably use either a uniform or adaptive grid for most problems. The uniform grid supported in Flash-X discretizes the physical domain by placing grid points at regular intervals defined by the geometry of the problem. The grid configuration remains unchanged throughout the simulation, and exactly one block is mapped per processor. An adaptive grid changes the discretization over the course of the computation, and several blocks can be mapped to each computational processor. Two AMR packages are currently supported in Flash-X for providing adaptive grid capbility. The block-structured oct-tree based AMR package, PARAMESH has been the work horse since the beginning of the code. Support for AMReX is a later addition, and mimics the oct-tree behavior of Paramesh for Flash-X . Because multiple different grids types are supported in Flash-X, the user must match up the correct IO alternative implementation with the correct Grid alternative implementation. The best way of ensuring the match up is to use predefined shortcuts such as “+ugio”, which makes sure that the appropriate branch of IO is included when the uniform grid is being used. Please see for more information. Also see for shortcuts useful for the Grid unit.

GridMain Data Structures

The Grid unit is the most extensive infrastructure unit in the Flash-X code, and it owns data that most other units wish to fetch and modify. Since the data layout in this unit has implications on the manageability and performance of the code, we describe it in some detail here.

Flash-X can be run with a grid discretization that assumes cell-centered data, face-centered data, or a combination of the two. Physical data resides multidimensional F90 arrays; cell-centered variables in unk, short for “unknowns”, and face-centered variables in arrays called facevarx, facevary, and facevarz, which contain the face-centered data along the x, y, and z dimensions, respectively. The cell-centered array unk is dimensioned as array(NUNK_VARS,nxb,nyb,nzb,blocks), where nxb, nyb, nzb are the spatial dimensions of a single block, and blocks is the number of blocks per processor, which is 1 for UG. The face-centered arrays have one extra data point along the dimension they are representing, for example facevarx is dimensioned as array(NFACE_VARS,nxb+1,nyb,nzb,blocks). The spatial dimensions nxb, nyb, nzb can either be fixed at setup time, or they may be determined at runtime. These two modes are referred to as FIXEDBLOCKSIZE and NONFIXEDBLOCKSIZE.

All values determined at setup time are defined as constants in a file Simulation.h generated by the setup tool. This file contains all application-specific global constants such as the number and naming of physical variables, number and naming of fluxes and species, etc. For cell-centered variables, the Grid unit also stores a variable type that can be retrieved using the Simulation/Simulation_getVarnameType routine; see for the syntax and meaning of the optional TYPE attribute that can be specified as part of a VARIABLE definition read by the setup tool.

Computational Domain

The size of the computational domain in physical units is specified at runtime through the (xmin, xmax) (ymin, ymax) (zmin, zmax) runtime parameters. When working with curvilinear coordinates (see below in ), the extrema for angle coordinates are specified in degrees. Internally all angles are represented in radians, so angles are converted to radians at Grid initialization. The physical domain is mapped into a computational domain at problem initialization through the initialization routines of the selected AMR package.

Boundary Conditions

Much of the Flash-X code within the Grid unit that deals with implementing boundary conditions has been organized into a separate subunit, GridBoundaryConditions. Note that the following aspects are still handled elsewhere:

• Recognition of bounday condition names as strings (in runtime parameters) and constants (in the source code); these are defined in RuntimeParameters/RuntimeParameters_mapStrToInt and in constants.h, respectively.

• Handling of user-defined boundary conditions; this should be implemented by code under the Simulation directory.

• Behavior of particles at a domain boundary. This is based on the boundary types described below, but their handling is implemented in GridParticles.

Although the GridBoundaryConditions subunit is included in a setup by default, it can be excluded (if no Config file “REQUIRES” it) by specifying -without-unit=Grid/GridBoundaryConditions. This will generally only make sense if all domain boundaries are to be treated as periodic. (All relevant runtime parameters xl_boundary_type etc. need to be set to “periodic” in that case.)

Boundary Condition Types

Boundary conditions are determined by the physical problem. Within Flash-X, the parallel structure of blocks means that each processor works independently. If a block is on a physical boundary, the guard cells are filled by calculation since there are no neighboring blocks from which to copy values. Boundaries are selected by setting runtime parameters such as xl_boundary_type (for the ‘left’ X –boundary) to one of the supported boundary types in flash.par. Even though the runtime parameters for specifying boundary condition types are strings, the Grid unit understands them as defined integer constants defined in the file constants.h, which contains all global constants for the code. The translation from the string specified in “flash.par” to the constant understood by the Grid unit is done by the routine RuntimeParameters/RuntimeParameters_mapStrToInt.

Flash-X. Boundary type ab may be replaced with \(a\)={x,y,z} for direction and \(b\)={l,r} for left/right edge. All boundary types listed except the last (user) have an implementation in GridBoundaryConditions.

To use any of the hydrostatic-f2* boundary conditions, the setup must include Grid/GridBoundaryConditions/Flash2HSE. This must usually be explicitly requested, for example with a line

REQUIRES Grid/GridBoundaryConditions/Flash2HSE

in the simulation directory’s Config file.

Flash-X. Boundary type ab may be replaced with a={x,y,z} for direction and b={l,r} for left/right edge. These boundary types are either reserved for implementation by users and/or future Flash-X versions for a specific purpose (as indicate by the remarks), or are for special uses within the Grid unit.

Boundary Conditions at Obstacles

The initial coarse grid of root blocks can be modified by removing certain blocks. This is done by providing a non-trivial implementation of Simulation/Simulation_defineDomain. Effectively this creates additional domain boundaries at the interface between blocks removed and regions still included. All boundary conditions other than periodic are possible at these additional boundaries, and are handled there in the same way as on external domain boundaries. This feature is only available with PARAMESH. See the documentation and example in Simulation/Simulation_defineDomain for more details and some caveats.

Implementing Boundary Conditions

Users may need to implement boundary conditions beyond those provided with Flash-X, and the GridBoundaryConditions subunit provides several ways to achieve this. Users can provide an implementation for the user boundary type; or can provide or override an implementation for one of the other recognized types.

The simple boundary condition types reflect, outflow, diode are implemented in the Grid_bcApplyToRegion .F90 file in GridBoundaryConditions. A users can add or modify the handling of some boundary condition types in a version of this file in the simulation directory, which overrides the regular version. There is, however, also the interface Grid_bcApplyToRegionSpecialized which by default is only provided as a stub and is explicitly intended to be implemented by users. A Grid_bcApplyToRegionSpecialized implementation gets called before Grid_bcApplyToRegion and can decide to either handle a specific combination of boundary condition type, direction, grid data structure, etc., or leave it to Grid_bcApplyToRegion. These calls operate on a region of one block’s cells at a time. Flash-X will pass additional information beyond that needed for handling simple boundary conditions to Grid_bcApplyToRegionSpecialized, in particular a block handle through which an implementation can retrieve coordinate information and access other information associated with a block and its cells.

The GridBoundaryConditions subunit also provides a simpler kind of interface if one includes GridBoundaryConditions/OneRow in the setup. When using this style of interface, users can implement guard cell filling one row at a time. Flash-X passes to the implementation one row of cells at a time, some of which are interior cells while the others represent guard cells outside the boundary that are to be modified in the call. A row here means a contiguous set of cells along a line perpendicular to the boundary surface. There are two versions of this interface: Grid_applyBCEdge is given only one fluid variable at a time, but can also handle data structures other than unk; whereas Grid_applyBCEdgeAllUnkVars handles all variables of unk along a row in one call. Cell coordinate information is included in the call arguments. Flash-X invokes these functions through an implementation of Grid_bcApplyToRegionSpecialized in GridBoundaryConditions/OneRow which acts as a wrapper. GridBoundaryConditions/OneRow also provides a default implementation of Grid_applyBCEdge (which implements the simple boundary conditions) and Grid_applyBCEdgeAllUnkVars (which calls Grid_applyBCEdge) each. Another implementation of Grid_applyBCEdgeAllUnkVars can be found in GridBoundaryConditions/OneRow/Flash2HSE, this one calls Grid_applyBCEdge or, for Flash-X-type hydrostatic boundaries, the code for handling them. These can be used as templates for overriding implementations under Simulation. It is not recommended to try to mix both Grid_bcApplyToRegion*-style and Grid_applyBCEdge*-style overriding implementations in a simulation directory, since this could become confusing.

Note that in all of these cases, i.e., whether boundary guard cell filling for a boundary type is implemented in Grid_bcApplyToRegion, Grid_bcApplyToRegionSpecialized, Grid_applyBCEdge, or Grid_applyBCEdgeAllUnkVars, the implementation does not fill guard cells in permanent data storage (the unk array and similar data structures) directly, but operates on buffers. Flash-X fills some parts of the buffers with current values for interior cells before the call, and copies updated guardcell data from some (other) parts of the buffers back into unk (or similar) storage after the handling routine returns.

The boundary condition handling interfaces described so far can be implemented (and will be used!) independent of the Grid implementation chosen. At a lower level, the various implementations of GridMain have different ways of requesting that boundary guard cells be filled. The GridBoundaryConditions subunit collaborates with GridMain implementations to provide to user code uniform interfaces that are agnostic of lower-level details. However, it is also possible — but not recommended — for users to replace a routine that is located deeper in the Grid unit.

Uniform Grid

The Uniform Grid has the same resolution in all the blocks throughout the domain, and each processor has exactly one block.

In FLASH, the uniform grid can operate in either of two modes: fixed block size (FIXEDBLOCKSIZE) mode, and non-fixed block size (NONFIXEDBLOCKSIZE) mode. The default fixed block size grid is statically defined at compile time and can therefore take advantage of compile-time optimizations. The non-fixed block size version uses dynamic memory allocation of grid variables. Flash-X currently only supports the Uniform Grid in NONFIXEDBLOCKSIZE mode (whereas the other Grid implementations in Flash-X operate in FIXEDBLOCKSIZE mode).

FIXEDBLOCKSIZE Mode

NOTE THAT THIS MODE IS CURRENTLY NOT IMPLEMENTED IN Flash-X. The remainder of this section thus is only for historical information.

FIXEDBLOCKSIZE mode, also called static mode, is the default for the uniform grid in FLASH. In this mode, the block size is specified at compile time as NXB\(\times\)NYB\(\times\)NZB. These variables default to \(8\) if the dimension is defined and \(1\) otherwise – e.g. for a two-dimensional simulation, the defaults are NXB\(=8\), NYB\(=8\), NZb\(=1\). To change the static dimensions, specify the desired values on the command line of the setup script; for example

./setup Sod -auto -3d -nxb=12 -nyb=12 -nzb=4 +ug

The distribution of processors along the three dimensions is given at run time as \(iprocs\times jprocs\times kprocs\) with the constraint that this product must be equal to the number of processors that the simulation is using. The global domain size in terms of number of grid points is \({\tt NXB}*iprocs \times {\tt NYB}*jprocs \times {\tt NZB}*kprocs\). For example, if \(iprocs=jprocs=4\) and \(kprocs=1\), the execution command should specify \(np=16\) processors.

mpirun -np 16 flashx

When working in static mode, the simulation is constrained to run on the same number of processors when restarting, since any different configuration of processors would change the domain size.

At Grid initialization time, the domain is created and the communication machinery is also generated. This initialization includes MPI communicators and datatypes for directional guardcell exchanges. If we view processors as arranged in a three-dimensional processor grid, then a row of processors along each dimension becomes a part of the same communicator. We also define MPI datatypes for each of these communicators, which describe the layout of the block on the processor to MPI. The communicators and datatypes, once generated, persist for the entire run of the application. Thus the MPI_SEND/RECV function with specific communicator and its corresponding datatype is able to carry out all data exchange for guardcell fill in the selected direction in a single step.

Since all blocks exist at the same resolution in the Uniform Grid, there is no need for interpolation while filling the guardcells. Simple exchange of correct data between processors, and the application of boundary conditions where needed is sufficient. The guard cells along the face of a block are filled with the layers of the interior cells of the block on the neighboring processor if that face is shared with another block, or calculated based upon the boundary conditions if the face is on the physical domain boundary. Also, because there are no jumps in refinement in the Uniform Grid, the flux conservation step across processor boundaries is unnecessary. For correct functioning of the Uniform Grid in Flash-X, this conservation step should be explicitly turned off with a runtime parameter flux_correct which controls whether or not to run the flux conservation step in the PPM Hydrodynamics implementation. AMR sets it by default to true, while UG sets it to false. Users should exercise care if they wish to override the defaults via their flash.par file.

NONFIXEDBLOCKSIZE mode

To run an application in “NONFIXEDBLOCKSIZE” mode the “-nofbs” option must be used when invoking the setup tool; For example:

./setup Sod -3d -auto -nofbs

Note that NONFIXEDBLOCKSIZE mode requires the use of its own IO implementation, and a convenient shortcut has been provided to ensure that this mode is used as in the example below:

./setup Sod -3d -auto +nofbs

In this mode, the blocksize in UG is determined at execution from runtime parameters iGridSize, jGridSize and kGridSize. These parameters specify the global number of grid points in the computational domain along each dimension. The blocksize then is \((iGridSize/iprocs)\times(jGridSize/jprocs)\times(kGridSize/kprocs)\).

Unlike FIXEDBLOCKSIZE mode, where memory is allocated at compile time, in the NONFIXEDBLOCKSIZE mode allocation is dynamic. The example shown below gives two possible ways to define parameters in flash.par for a 3d problem of global domain size \(64 \times 64 \times 64\), being run on 8 processors.

iprocs = 2 jprocs = 2 kprocs = 2 iGridSize = 64 jGridSize = 64 kGridSize = 64

This specification will result in each processor getting a block of size \(32 \times 32 \times 32\). Now consider the following specification for the number of processors along each dimension, keeping the global domain size the same.

iprocs = 4 jprocs = 2 kprocs = 1

In this case, each processor will now have blocks of size \(16 \times 32 \times 64\).

Adaptive Mesh Refinement (AMR) Grid

Flash-X uses block-structured AMR where the fundamental data structure is a block of cells arranged in a logically Cartesian fashion. “Logically Cartesian” implies that each cell can be specified using a block identifier (processor number and local block number) and a coordinate triple \((i,j,k)\), where \(i=1\ldots{\tt nxb}\), \(j=1\ldots{\tt nyb}\), and \(k=1\ldots{\tt nzb}\) refer to

the \(x\)-, \(y\)-, and \(z\)-directions, respectively. It does not require a physically rectangular coordinate system; for example a spherical grid can be indexed in this same manner.

The complete computational grid consists of a collection of blocks with different physical cell sizes, which are related to each other in a hierarchical fashion resembling an oct-tree. The tree with parent-child relationship is native to Paramesh, however, in Flash-X, AMReX also mimics the oct-tree organization. Three rules govern the establishment of refined child blocks in Flash-X. First, a refined child block must be one-half as large as its parent block in each spatial dimension. Second, a block’s children must be nested; i.e., the child blocks must fit within their parent block and cannot overlap one another, and the complete set of children of a block must fill its volume. Thus, in \(d\) dimensions a given block has either zero or \(2^d\) children. Third, blocks which share a common border may not differ from each other by more than one level of refinement.

A simple two-dimensional domain is shown in , illustrating the rules above. Each block contains \({\tt nxb}\times{\tt nyb}\times{\tt nzb}\) interior cells and a set of guard cells. The guard cells contain boundary information needed to update the interior cells. These can be obtained from physically neighboring blocks, externally specified boundary conditions, or both.

|image1|

The number of guard cells needed depends upon the interpolation schemes and the differencing stencils used by the various physics units (usually hydrodynamics). The blocksize while using the adaptive grid is assumed to be known at compile time, though it is not strictly necessary for AMReX. When using Paramesh the total number of blocks a processor can manage is determined by MAXBLOCKS which can be overridden at setup.

AMR handles the filling of guard cells with information from other blocks or, at the boundaries of the physical domain, from an external boundary routine. If a block’s neighbor exists and has the same level of refinement, corresponding guard cells are filled using a direct copy from the neighbor’s interior cells. If the neighbor has a different level of refinement, the data from the neighbor’s cells must be adjusted by either interpolation (to a finer level of resolution) or averaging (to a coarser level) parallel communications take place (blocks are never split between processors). The filling of guard cells is a global operation that is triggered by calling Grid_fillGuardCells

Grid Interpolation is also used when filling the cells of newly created finer blocks during refinement. AMR also enforces flux conservation at jumps in refinement, as described by Berger and Colella (1989). At jumps in refinement, the fluxes of mass, momentum, energy (total and internal), and species density in the fine cells across boundary cell faces are summed and replace the corresponding fluxes in the boundary cells of their neighbors at coarser level of resolution. The summing allows a geometrical weighting to be implemented for non-Cartesian geometries, which ensures that the proper volume-corrected flux is computed.

Grid Interpolation (and Averaging)

The adaptive grid requires data interpolation or averaging when the refinement level (i.e., mesh resolution) changes in space or in time. [3]_ If during guardcell filling a block’s neighbor has a coarser level of refinement, the neighbor’s cells are used to interpolate guard cell values to the cells of the finer block. Interpolation is also used when filling the blocks of children newly created in the course of automatic refinement. Data averaging is used to adapt data in the opposite direction, i.e., from fine to coarse.

In the AMR context, the term prolongation is used to refer to data interpolation (because it is used when the tree of blocks grows longer). Similarly, the term restriction is used to refer to fine-to-coarse data averaging.

The algorithm used for restriction is straightforward (equal-weight) averaging in Cartesian coordinates, but has to take cell volume factors into account for curvilinear coordinates; see .

Both AMReX and Paramesh support various interpolation schemes, to which user-specified interpolation schemes can be added. When using Paramesh, Flash-X currently allows to choose between two interpolation schemes:

1. monotonic

2. native

The choice is made at setup time.

Interpolation for mass-specific solution variables

To accurately preserve the total amount of conserved quantities, the interpolation routines have to be applied to solution data in conserved, i.e., volume-specific, form. However, many variables are usually stored in the*unk array in mass-specific form, e.g., specific internal and total energies, velocities, and mass fractions.

Flash-X provides three ways to deal with this:

1. Do nothing—i.e., assume that ignoring the difference between mass-specific and conserved form is a reasonable approximation. Depending on the smoothness of solutions in regions where refinement, derefinement, and jumps in refinement level occur, this assumption may be acceptable. This behavior can be forced by setting the convertToConsvdInMeshInterp runtime parameter to .false.

2. Convert mass-specific variables to conserved form in all blocks throughout the physical domain before invoking a Grid function that may result in some data interpolation or restriction (refinement, derefinement, guardcell filling); and convert back after these functions return. Conversion is done by cell-by-cell multiplication with the density (i.e., the value of the “dens” variable, which should be declared as

   VARIABLE dens TYPE: PER_VOLUME

   This behavior is available in Paramesh and is enabled by setting the convertToConsvdForMeshCalls runtime parameter and corresponds roughly to Flash-X with conserved_var enabled.

3. Convert mass-specific variables to conserved form only where and when necessary, from the Grid user’s point of view as part of data interpolation. Again, conversion is done by cell-by-cell multiplication with the value of density. In the actual implementation of this approach, the conversion and back-conversion operations are closely bracketing the interpolation (or restriction) calls. The implementation avoids spurious back-and-forth conversions (i.e., repeated successive multiplications and divisions of data by the density) in blocks that should not be modified by interpolation or restriction.

   This behavior is available only for Paramesh.

Refinement

Refinement Criteria

The refinement criterion used by Flash-X is adapted from Löhner (1987). Löhner’s error estimator was originally developed for finite element applications and has the advantage that it uses a mostly local calculation. Furthermore, the estimator is dimensionless and can be applied with complete generality to any of the field variables of the simulation or any combination of them.

Flash-X does not define any refinement variables by default. Therefore simulations using AMR have to make the appropriate runtime parameter definitions in flash.par, or in the simulation’s Config file. If this is not done, the program generates a warning at startup, and no automatic refinement will be performed. The mistake of not specifying refinement variables is thus easily detected. To define a refinement variable, use refine_var_# (where # stands for a number from 1 to 4) in the flash.par file.

Löhner’s estimator is a modified second derivative, normalized by the average of the gradient over one computational cell. In one dimension on a uniform mesh, it is given by

\[E_{i} = { \frac{ \mid u_{i+1} - 2u_{i} + u_{i-1} \mid} % \over { \mid u_{i+1} - u_{i} \mid + \mid u_{i} - u_{i-1} \mid + \epsilon [ \mid u_{i+1} \mid + 2 \mid u_{i} \mid + \mid u_{i-1} \mid ] }\ } , %E_{i} = { \mid u_{i+1} - 2u_{i} + u_{i-1} \mid % \over % warning about Foreign over from amsmath % \mid u_{i+1} - u_{i} \mid + \mid u_{i} - u_{i-1} \mid + % \epsilon [ \mid u_{i+1} \mid + 2 \mid u_{i} \mid + % \mid u_{i-1} \mid ] }\ ,\]

where \(u_i\) is the refinement test variable’s value in the \(i\)th cell. The last term in the denominator of this expression acts as a filter, preventing refinement of small ripples, where \(\epsilon\) should be a small constant.

When extending this criterion to multidimensions, all cross derivatives are computed, and the following generalization of the above expression is used

\[E_{i_1i_2i_3} = \left\{ {\displaystyle % \sum_{pq}\left({\partial^2 u\over\partial x_p\partial x_q} \sum_{pq}\left({ \frac{\partial^2 u}{\partial x_p\partial x_q}} \Delta x_p\Delta x_q\right)^2 } \over {\displaystyle \sum_{pq}\left[\left( \left|{\partial u\over\partial x_p}\right|_{i_p+1/2} + \left|{\partial u\over\partial x_p}\right|_{i_p-1/2} \right)\Delta x_p + \epsilon{\partial^2 |u|\over \partial x_p\partial x_q} \Delta x_p\Delta x_q \right]^2 } \right\}^{1/2},\]

where the sums are carried out over coordinate directions, and where, unless otherwise noted, partial derivatives are evaluated at the center of the \(i_1i_2i_3\)-th cell.

The estimator actually used in Flash-X’s default refinement criterion is a modification of the above, as follows:

\[E_{i} = { \mid u_{i+2} - 2u_{i} + u_{i-2} \mid \over \mid u_{i+2} - u_{i} \mid + \mid u_{i} - u_{i-2} \mid + \epsilon [ \mid u_{i+2} \mid + 2 \mid u_{i} \mid + \mid u_{i-2} \mid ] }\ ,\]

where again \(u_i\) is the refinement test variable’s value in the \(i\)th cell. The last term in the denominator of this expression acts as a filter, preventing refinement of small ripples, where \(\epsilon\) is a small constant.

When extending this criterion to multidimensions, all cross derivatives are computed, and the following generalization of the above expression is used

\[E_{i_Xi_Yi_Z} = \left\{ {\displaystyle \sum_{pq}\left({\partial^2 u\over\partial x_p\partial x_q} \right)^2 } \over {\displaystyle \sum_{pq}\left[ \frac{1}{2\,\Delta x_q}\left( \left|{\partial u\over\partial x_p}\right|_{i_q+1} + \left|{\partial u\over\partial x_p}\right|_{i_q-1} \right) + \epsilon{\bar{\left|u_{pq}\right|}\over \Delta x_p\Delta x_q} \right]^2 } \right\}^{1/2},\]

where again the sums are carried out over coordinate directions, where, unless otherwise noted, partial derivatives are actually finite-difference approximations evaluated at the center of the \(i_Xi_Ji_K\)-th cell, and \(\bar{\left|u_{pq}\right|}\) stands for an average of the values of \(\left|u\right|\) over several neighboring cells in the \(p\) and \(q\) directions.

The constant \(\epsilon\) is by default given a value of \(10^{-2}\), and can be overridden through the refine_filter_# runtime parameters. Blocks are marked for refinement when the value of \(E_{i_Xi_Yi_Z}\) for any of the block’s cells exceeds a threshold given by the runtime parameters refine_cutoff_#, where the number # matching the number of the refine_var_# runtime parameter selecting the refinement variable. Similarly, blocks are marked for derefinement when the values of \(E_{i_Xi_Yi_Z}\) for all of the block’s cells lie below another threshold given by the runtime parameters derefine_cutoff_#.

When Particles (active or tracer) are being used in a simulation, their count in a block can also be used as a refinement criterion by setting refine_on_particle_count to true and setting max_particles_per_blk to the desired count.

Refinement Processing

Each processor decides when to refine or derefine its blocks by computing a user-defined error estimator for each block. Refinement involves creation of either zero or \(2^d\) refined child blocks, while derefinement involves deletion of all of a parent’s child blocks (\(2^d\) blocks). As child blocks are created, they are temporarily placed at the end of the processor’s block list. After the refinements and derefinements are complete, the blocks are redistributed among the processors using a work-weighted Morton space-filling curve in a manner similar to that described by Warren and Salmon (1987) for a parallel treecode. An example of a Morton curve is shown in .

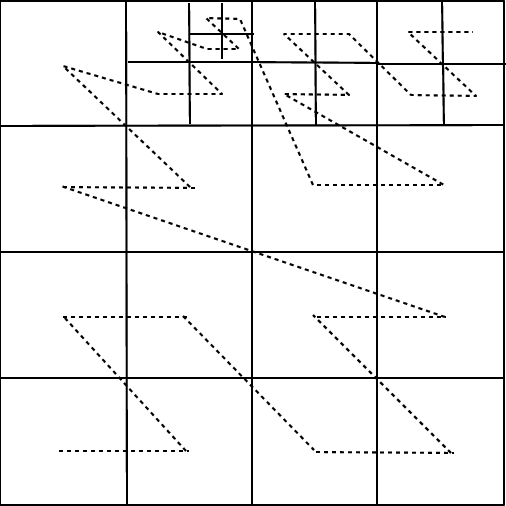
Morton space-filling curve for adaptive mesh grids.

During the distribution step, each block is assigned a weight which estimates the relative amount of time required to update the block. The Morton number of the block is then computed by interleaving the bits of its integer coordinates, as described by Warren and Salmon (1987). This reordering determines its location along the space-filling curve. Finally, the list of all blocks is partitioned among the processors using the block weights, equalizing the estimated workload of each processor. By default, all leaf-blocks are weighted twice as heavily as all other blocks in the simulation.

Specialized Refinement Routines

Sometimes, it may be desirable to refine a particular region of the grid independent of the second derivative of the variables. This criterion might be, for example, to better resolve the flow at the boundaries of the domain, to refine a region where there is vigorous nuclear burning, or to better resolve some smooth initial condition. For curvilinear coordinates, regions around the coordinate origin or the polar \(z\)-axis may require special consideration for refinement. A collection of methods that can refine a (logically) rectangular region or a circular region in Cartesian coordinates, or can automatically refine by using some variable threshold, are available through the Grid_markRefineSpecialized. It is intended to be called from the Grid_markRefineDerefine routine. The interface works by allowing the calling routine to pick one of the routines in the suite through an integer argument. The calling routine is also expected to populate the data structure specs before making the call. A copy of the file Grid_markRefineDerefine.F90 should be placed in the Simulation directory.

GridMain Usage

The Grid unit has the largest API of all units, since it is the custodian of the bulk of the simulation data, and is responsible for most of the code housekeeping. The *Grid_init routine, like all other Unit_init routines, collects the runtime parameters needed by the unit and stores values in the data module. If using UG, the Grid_init also creates the computational domain and the housekeeping data structures and initializes them. If using AMR, the computational domain is created by the Grid_initDomain routine, which also makes a call to mesh package’s own initialization routine. The physical variables are all owned by the Grid unit, and it initializes them by calling the Simulation/Simulation_initBlock routine which applies the specified initial conditions to the domain. If using an adaptive grid, the initialization routine also goes through a few refinement iterations to bring the grid to desired initial resolution, and then applies the physics/Eos/Eos function to bring all simulation variables to thermodynamic equilibrium. Even though the mesh-based variables are under Grid’s control, all the physics units can operate on and modify them.

In Flash-X the Grid unit implements iterators that hand blocks or tiles to the physics solvers along with all the meta information that the physics solvers may need. The unit also provides a collection of routines that invoke some housekeeping functions of the grid without explicitly fetching any data. A good example of such routines is Grid_fillGuardCells. Here no data transaction takes place between Grid and the calling unit. The calling unit simply instructs the Grid unit that it is ready for the guard cells to be updated, and doesn’t concern itself with the details. The Grid_fillGuardCells routine makes sure that all the blocks get the right data in their guardcells from their neighbors, whether they are at the same, lower or higher resolution, and if instructed by the calling routine, also ensures that EOS is applied to them.

Another routine that may change the global state of the grid is Grid_updateRefinement. This function is called when the client unit wishes to update the grid’s resolution. again, the calling unit does not need to know any of the details of the refinement process.

As mentioned in , Flash-X allows every unit to identify scalar variables for checkpointing. In the Grid unit, the function that takes care of consolidating user specified checkpoint variable is Grid_sendOutputData. Users can select their own variables to checkpoint by including an implementation of this function specific to their requirements in their Simulation setup directory.

GridParticles

Flash-X is primarily an Eulerian code, however, there is support for tracing the flow using Lagrangian particles. In Flash-X we have generalized the interfaces in the Lagrangian framework of the Grid unit in such a way that it can also be used for miscellaneous non-Eulerian data such as tracing the path of a ray through the domain, or tracking the motion of solid bodies immersed in the fluid. Flash-X can also uses active particles with mass (though that features is not in the code yet), Each particle has an associated data structure, which contains fields such as its physical position and velocity, and relevant physical attributes such as mass or field values in active particles. Depending upon the time advance method, there may be other fields to store intermediate values. Also, depending upon the requirements of the simulation, other physical variables such as temperature etc.  may be added to the data structure. The GridParticles subunit of the Grid unit has two sub-subunits of its own. The GridParticlesMove sub-subunit moves the data structures associated with individual particles when the particles move between blocks; the actual movement of the particles through time advancement is the responsibility of the Particles unit. Particles move from one block to another when their time advance places them outside their current block. In AMR, the particles can also change their block through the process of refinement and derefinement. The GridParticlesMap sub-subunit provides mapping between particles data and the mesh variables. The mesh variables are either cell-centered or face-centered, whereas a particle’s position could be anywhere in the cell. The GridParticlesMap sub-subunit calculates the particle’s properties at its position from the corresponding mesh variable values in the appropriate cell . When using active particles, this sub-subunit also maps the mass of the particles onto the specified mesh variable in appropriate cells. The next sections describe the algorithms for moving and mapping particles data.

GridParticlesMove

Particles move between blocks under two circumstances. One is when time integration moves their physical location out of the current block, which is application to both UG and AMR, and the second is during refinement of the grid in AMR.

Directional Move

The Directional Move algorithm for moving particles in a Uniform Grid minimizes the number of communication steps instead of minimizing the volume of data moved. Its implementation has the following steps:

1. Scan particle positions. Place all particles with their \(x\) coordinate value greater than the block bounding box in the Rightmove bin, and place those with \(x\) coordinate less than block bounding box in Leftmove bin.

2. Exchange contents of Rightbin with the right block neighbor’s Leftbin contents, and those of the Leftbin with left neightbor’s Rightbin contents.

3. Merge newly arrived particles from step 2 with those which did not move outside their original block.

4. Repeat steps 1-3 for the y direction.

5. Repeat step 1-2 for the z direaction.

At the end of these steps, all particles will have reached their destination blocks, including those that move to a neighbor on the corner. illustrates the steps in getting a particle to its correct destination.

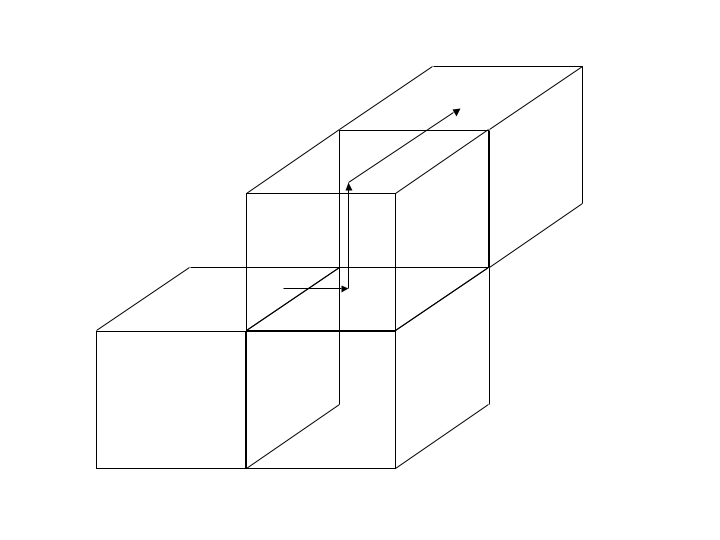
Moving one particle to a neighbor on the corner.

AMR Algorithm

When using AMReX one can opt to use its native particles support, in which case the handling of particles is largely transparent to Flash-X. Alternatively, one can use a point-to-point algorithm which exploits the bitmap of the mesh maintained by the Bittree that is available on every processor. Thus it is possible to determine the processor and block number of the destination block for each particle. The PointToPoint implementation finds out the destinations for every particles that is getting displaced from its block. Particles going to local destination blocks are moved first. The remaining particles are sorted based on their destination processor number, followed by a couple of global operations that allow every processor to determine the number of particles it is expected to receive from all of the other processors. A processor then posts asynchronous receives for every source processor that had at least one particle to send to it. In the next step, the processor cycles through the sorted list of particles and sends them to the appropriate destinations using synchronous mode of communition.

GridSolvers

The GridSolvers unit groups together subunits that are used to solve particular types of differential equations. .. Sec:GridSolversPoisson:

Poisson equation

The GridSolvers subunit contains several different algorithms for solving the general Poisson equation for a potential \(\phi({\bf x})\) given a source \(\rho({\bf x})\)

\[\label{Eqn:general Poisson} \nabla^2\phi({\bf x}) = \alpha\rho({\bf x})\ .\]

Here \(\alpha\) is a constant that depends upon the application. For example, when the gravitational Poisson equation is being solved, \(\rho({\bf x})\) is the mass density, \(\phi({\bf x})\) is the gravitational potential, and \(\alpha = 4\pi G\), where \(G\) is Newton’s gravitational constant.

Multipole Poisson solver

The multipole Poisson solver is based on a multipolar expansion of the source (mass for gravity, for example) distribution around a conveniently chosen center of expansion. The angular number \(L\) entering this expansion is a measure of how detailed the description of the source distribution will be on an angular basis. Higher \(L\) values mean higher angular resolution with respect to the center of expansion. The multipole Poisson solver is thus appropriate for spherical or nearly-spherical source distributions with isolated boundary conditions. For problems which require high spatial resolution throughout the entire domain (like, for example, galaxy collision simulations), the multipole Poisson solver is less suited, unless one is willing to go to extremely (computationally unfeasible) high \(L\) values. For stellar evolution, however, the multipole Poisson solver is the method of choice.

The multipole Poisson solver is located in the directory

source/Grid/GridSolvers/Multipole_new.

Details about the theory of this implementation of the Poisson solver can be found in Couch et al. (2013).

The multipole Poisson solver is appropriate for spherical or nearly-spherical source distributions with isolated boundary conditions. It currently works in 1D spherical, 2D spherical, 2D cylindrical, 3D Cartesian and 3D cylindrical. Symmetries can be specified for the 2D spherical and 2D cylindrical cases (a horizontal symmetry plane along the radial axis) and the 3D Cartesian case (assumed axisymmetric property). Because of the radial symmetry in the 1D spherical case, only the monopole term (\(\ell = 0\)) contributes, while for the 3D Cartesian axisymmetric, the 2D cylindrical and 2D spherical cases only the \(m = 0\) moments need to be used (the other \(m\neq 0\) moments effectively cancel out).

The multipole algorithm consists of the following steps. First, the center of the multipolar expansion \({\bf x}_{\rm cen}\) is determined via density-squared weighted integration over position:

\[{\bf x}_{\rm cen} = {\int {\bf x}\rho^2({\bf x})\,d{\bf x} \over \int \rho^2({\bf x})\,d{\bf x}}.\]

We will take \({\bf x}_{\rm cen}\) as our origin. In integral form, Poisson’s equation ([Eqn:general Poisson]) becomes

\[\label{Eqn:PoissonIntegral} \phi({\bf x}) = -{\alpha\over 4\pi}\int {\rho({\bf x}')\over |{\bf x} - {\bf x}'|}\,d{\bf x}'.\]

The inverse radial distance part can be expanded in terms of Legendre polynomials

\[\label{Eqn:Inverse distance Legendre} {1\over |{\bf x} - {\bf x}'|} = \sum_{\ell=0}^\infty {x_<^\ell\over x_>^{\ell+1}}P_\ell (\cos\gamma),\]

where \(x_<\) (\(x_>\)) indicate the smaller (larger) of the magnitudes and \(\gamma\) denotes the angle between \({\bf x}\) and \({\bf x}'\). Note, that this definition includes those cases where both magnitudes are equal. The expansion is always convergent if \(\cos\gamma <1\). Expansion of the Legendre polynomials in terms of spherical harmonics gives

\[\label{Eqn:Legendre spherical harmonics} P_\ell (\cos\gamma) = {4\pi\over 2\ell+1}\sum_{m=-\ell}^{+\ell} Y_{\ell m}^*(\theta',\phi') Y_{\ell m}(\theta,\phi),\]

where \(\theta,\phi\) and \(\theta',\phi'\) are the spherical angular components of \({\bf x}\) and \({\bf x}'\) about \({\bf x}_{\rm cen}\). Defining now the regular \(R_{\ell m}\) and irregular \(I_{\ell m}\) solid harmonic functions

\[\begin{split}\begin{aligned} R_{\ell m}(x_<) & = & \sqrt{{4\pi\over {2\ell+1}}}x_<^\ell Y_{\ell m}(\theta,\phi) \\ I_{\ell m}(x_>) & = & \sqrt{{4\pi\over {2\ell+1}}}{Y_{\ell m}(\theta,\phi)\over x_>^{\ell+1}},\end{aligned}\end{split}\]

we can rewrite Eq.([Eqn:PoissonIntegral]) in the form

\[\label{Eqn:Poisson solid harmonics} \phi({\bf x}) = -{\alpha\over 4\pi} \int \sum_{\ell m}R_{\ell m}(x_<)I_{\ell m}^*(x_>)\rho({\bf x}')\,d{\bf x}',\]

where the summation sign is a shorthand notation for the double sum over all the allowed \(\ell\) and \(m\) values. In Flash-X both the source and the potential are assumed to be cell-averaged quantities discretized on a block-structured mesh with varying cell size. The integration must hence be replaced by a summation over all leaf cells

\[\label{Eqn:Poisson discrete incorrect} \phi(q) = -{\alpha\over 4\pi} \sum_{q'} \sum_{\ell m}R_{\ell m}(q_<)I_{\ell m}^*(q_>)m(q'),\]

where \(m\) denotes the cell’s mass. Note, that the symbol \(q\) stands for cell index as well as its defining distance position from the expansion center in the computational domain. This discrete Poisson equation is incorrect. It contains the divergent \(q'=q\) term on the rhs. The \(q'=q\) contribution to the potential corresponds to the cell self potential \(\phi_{Self}(q)\) and is divergent in our case because all the cell’s mass is assumed to be concentrated at the cell’s center. The value of this divergent term can easily be calculated from Eq.([Eqn:Inverse distance Legendre]) by setting \(\cos\gamma = 1\):

\[\begin{aligned} \phi_{Self}(q) & = & m(q){L+1\over x_q},\end{aligned}\]

where \(m\) is the cell’s mass, \(L\) the highest angular number considered in the expansion and \(x_q\) the radial distance of the cell center from the expansion center. To avoid this divergence problem, we evaluate the potentials on each face of the cell and form the average of all cell face potentials to get the cell center potential. Eq.([Eqn:Poisson discrete incorrect]) will thus be replaced by

\[\phi(q) = {1\over n_F} \sum_{F} \phi({\bf x}_F)\]

and

\[\label{Eqn:Poisson discrete correct} \phi({\bf x}_F) = -{\alpha\over 4\pi} \sum_{q'} \sum_{\ell m}R_{\ell m}([q',x_F]_<)I_{\ell m}^*([q',x_F]_>)m(q'),\]

where \({\bf x}_F\) is the cell face radial distance from the expansion center and \([q',x_F]_<\) denotes the larger of the magnitudes between the cell center radial distance \(q'\) and the cell face radial distance \(x_F\). Splitting the summation over cells in two parts

\[\label{Eqn:Poisson discrete correct 1} \phi({\bf x}_F) = -{\alpha\over 4\pi}\left\{ \sum_{q'\leq x_F} \sum_{\ell m}\left[R_{\ell m}(q')m(q')\right]I_{\ell m}^*({\bf x}_F) + \sum_{q'>x_F} \sum_{\ell m}R_{\ell m}({\bf x}_F)\left[I_{\ell m}^*(q')m(q')\right]\right\},\]

and defining the two moments

\[\begin{split}\begin{aligned} M^R_{\ell m}({\bf x}_F) & = & \sum_{q'\leq x_F} R_{\ell m}(q')m(q') \label{Eqn:Moment definition 1} \\ M^I_{\ell m}({\bf x}_F) & = & \sum_{q'>x_F} I_{\ell m}(q')m(q'),\label{Eqn:Moment definition 2}\end{aligned}\end{split}\]

we obtain

\[\label{Eqn:Poisson discrete correct 2} \phi({\bf x}_F) = -{\alpha\over 4\pi}\left[ \sum_{\ell m}M^R_{\ell m}({\bf x}_F)I_{\ell m}^*({\bf x}_F) + \sum_{\ell m}M^{I*}_{\ell m}({\bf x}_F)R_{\ell m}({\bf x}_F)\right]\]

and using vector notation

\[\label{Eqn:Poisson discrete correct 3} \phi({\bf x}_F) = -{\alpha\over 4\pi}\left[ {\bf M}^R({\bf x}_F)\cdot {\bf I}^*({\bf x}_F) + {\bf M}^{I*}({\bf x}_F)\cdot {\bf R}({\bf x}_F) \right].\]

We now change from complex to real formulation. We state this for the regular solid harmonic functions, the same reasoning being applied to the irregular solid harmonic functions and all their derived moments. The regular solid harmonic functions can be split into a real and imaginary part

\[\label{Eqn:Solid harmonics real} R_{\ell m} = R_{\ell m}^c + i\,R_{\ell m}^s.\]

The labels ’c’ and ’s’ are shorthand notations for ’cosine’ and ’sine’, reflecting the nature of the azimuthal function of the corresponding real spherical harmonics. When inserting ([Eqn:Solid harmonics real]) into ([Eqn:Poisson discrete correct 3]) all cosine and sine mixed terms of the scalar products cancel out. Also, due to the symmetry relations

\[\begin{split}\begin{aligned} R_{\ell,-m}^c & = & (-1)^m R_{\ell m}^c \\ R_{\ell,-m}^s & = & -(-1)^m R_{\ell m}^s\end{aligned}\end{split}\]

we can restrict ourselves to the following polar angle number ranges

\[\begin{split}\begin{aligned} c & : & \ell\geq 0\;\;,\;\;\ell\geq m \geq 0 \\ s & : & \ell\geq 1\;\;,\;\;\ell\geq m \geq 1.\end{aligned}\end{split}\]

The real formulation of ([Eqn:Poisson discrete correct 3]) becomes then

\[\begin{split}\label{Eqn:Poisson discrete correct real} \phi({\bf x}_F) = -{\alpha\over 4\pi}\left\{ \left[\begin{array}{l} {\bf M}^{Rc}({\bf x}_F) \\ {\bf M}^{Rs}({\bf x}_F) \end{array}\right] \cdot {\bf \Delta} \left[\begin{array}{l} {\bf I}^c({\bf x}_F) \\ {\bf I}^s({\bf x}_F) \end{array}\right] + \left[\begin{array}{l} {\bf M}^{Ic}({\bf x}_F) \\ {\bf M}^{Is}({\bf x}_F) \end{array}\right] \cdot {\bf \Delta} \left[\begin{array}{l} {\bf R}^c({\bf x}_F) \\ {\bf R}^s({\bf x}_F) \end{array}\right]\right\},\end{split}\]

which, when compared to ([Eqn:Poisson discrete correct 3]), shows, that all vectors now contain a cosine and a sine section. The \({\bf \Delta}\) matrix is a diagonal matrix whose elements are equal to 2 for \(m\neq 0\) and 1 otherwise, i.e.:

\[\label{Eqn:Delta matrix} {\bf \Delta} = diag(2-\delta_{m0}).\]

The recursion relations for calculating the solid harmonic vectors are

\[\begin{split}\begin{aligned} R_{00}^c & = & 1 \label{Eqn:Regular Recurrence} \\ R_{\ell\ell}^c & = & - {xR_{\ell-1,\ell-1}^c-yR_{\ell-1,\ell-1}^s\over 2\ell}\\ R_{\ell\ell}^s & = & - {yR_{\ell-1,\ell-1}^c+xR_{\ell-1,\ell-1}^s\over 2\ell}\\ R_{\ell m}^{c/s} & = & {(2\ell - 1)zR_{\ell-1,m}^{c/s}-r^2R_{\ell-2,m}^{c/s} \over (\ell + m)(\ell - m)},\;\;\;0\leq m <\ell\end{aligned}\end{split}\]

and

\[\begin{split}\begin{aligned} I_{00}^c & = & {1\over r} \\ I_{\ell\ell}^c & = & - (2\ell-1){xI_{\ell-1,\ell-1}^c-yI_{\ell-1,\ell-1}^s\over r^2} \\ I_{\ell\ell}^s & = & - (2\ell-1){yI_{\ell-1,\ell-1}^c+xI_{\ell-1,\ell-1}^s\over r^2} \\ I_{\ell m}^{c/s} & = & {(2\ell - 1)zI_{\ell-1,m}^{c/s}-\left[(\ell-1)^2-m^2\right] I_{\ell-2,m}^{c/s}\over r^2},\;\;\;0\leq m <\ell \label{Eqn:Irregular Recurrence}\end{aligned}\end{split}\]

in which \(x,y,z\) are the cartesian location coordinates of the cell face and \(r^2=x^2+y^2+z^2\). For geometries depending on polar angles one must first calculate the corresponding cartesian coordinates for each cell before applying the recursions. In Flash-X, the order of the two cosine and sine components for each solid harmonic vector is such that \(\ell\) precedes \(m\). This allows buildup of the vectors with maximum number of unit strides. The same applies of course for the assembly of the moments. For 2D cylindrical and 2D spherical geometries only the \(m=0\) parts of both recursions are needed, involving only the cartesian \(z\) coordinate and \(r^2\). Symmetry along the radial axes of these 2D geometries inflicts only the sign change \(z\rightarrow -z\), resulting in the symmetry relations \(R_{\ell 0}^c\rightarrow R_{\ell 0}^c\) for even \(\ell\) and \(R_{\ell 0}^c\rightarrow -R_{\ell 0}^c\) for odd \(\ell\), the same holding for the irregular solid harmonic vector components. Thus symmetry in 2D can effectively be treated by halving the domain size and multiplying each even \(\ell\) moments by a factor of 2 while setting the odd \(\ell\) moments equal to 0. For 3D cartesian geometries introduction of symmetry is far more complicated since all \(m\) components need to be taken into account. It is not sufficient to simply reduce the domain to the appropriate size and multiply the moments by some factor, but rather one would have to specify the exact symmetry operations intended (generators of the symmetry group \(O_h\) or one of its subgroups) in terms of their effects on the \(x,y,z\) cartesian basis. The resulting complications in calculating symmetry adapted moments outweighs the computational gain that can be obtained from it. Options for 3D symmetry are thus no longer available in the improved Flash-X multipole solver. The ’octant’ symmetry option from the old multipole solver, using only the monopole \(\ell=0\) term, was too restrictive in its applicability (exact only for up to angular momenta \(\ell =3\) due to cancellation of the solid harmonic vector components).

From the above recursion relations ([Eqn:Regular Recurrence]-[Eqn:Irregular Recurrence]), the solid harmonic vector components are functions of \(x^iy^jz^k\) monomials, where \(i+j+k=\ell\) for the \({\bf R}\) and (formally) \(i+j+k=-(\ell+1)\) for the \({\bf I}\). For large astrophysical coordinates and large \(\ell\) values this leads to potential computational over- and underflow. To get independent of the size of both the coordinates and \(\ell\) we introduce a damping factor \(Dx,Dy,Dz\) for the coordinates for each solid harmonic type before entering the recursions. \(D\) will be chosen such that for the highest specified \(\ell=L\) we will have approximately a value close to 1 for both solid harmonic components:

\[\begin{split}\begin{aligned} R^{c/s}_{Lm} & \approx & 1 \label{Eqn:Damping condition 1} \\ I^{c/s}_{Lm} & \approx & 1.\label{Eqn:Damping condition 2}\end{aligned}\end{split}\]

This ensures proper handling of size at the solid harmonic function evaluation level and one does not have to rely on size cancellations at a later stage when evaluating the potential via Eq.([Eqn:Poisson discrete correct real]). We next state the evaluation of the damping factor \(D\). Due to the complicated nature of the recursions, the first step is to find solid harmonic components which have a simple structure. To do this, consider a cell face with \(x,y=0\) and \(z\neq 0\). Then \(r^2=z^2\), \(|z|=r\) and only the \(m=0\) components are different from zero. An explicit form can be stated for the absolute values of these components in terms of \(r\):

\[\begin{split}\begin{aligned} \label{Eqn:Regular solid harmonic xy0} |R_{\ell 0}| & = & {r^\ell\over \ell!} \\ |I_{\ell 0}| & = & {\ell!\over r^{\ell+1}}. \label{Eqn:Irregular solid harmonic xy0}\end{aligned}\end{split}\]

Since \(r=\sqrt{x^2+y^2+z^2}\), damping of the coordinates with \(D\) results in a damped radial cell face distance \(Dr\). Inserting this result into ([Eqn:Regular solid harmonic xy0]) and ([Eqn:Irregular solid harmonic xy0]) and imposing conditions ([Eqn:Damping condition 1]) and ([Eqn:Damping condition 2]) results in

\[\begin{split}\begin{aligned} \label{Eqn:Damping components} D_R = {1\over r}\sqrt[L]{L!} & \approx & {1\over r}{L\over e}\sqrt[2L]{2\pi L}\\ D_I = {1\over r}\sqrt[L+1]{L!} & \approx & {1\over r}{L\over e}\sqrt[2L+2]{{2\pi e^2\over L}},\end{aligned}\end{split}\]

where the approximate forms are obtained by using Stirling’s factorial approximation formula for large \(L\). In Flash-X only the approximate forms are computed for \(D_R\) and \(D_I\) to avoid having to deal with factorials of large numbers.

From the moment defining equations ([Eqn:Moment definition 1]) and ([Eqn:Moment definition 2]) we see, that the moments are sums over subsets of cell center solid harmonic vectors multiplied by the corresponding cell mass. From Eq.([Eqn:Poisson discrete correct real]) it follows that for highest accuracy, the moments should be calculated and stored for each possible cell face. For high refinement levels and/or 3D simulations this would result in an unmanageable request for computer memory. Several cell face positions have to be bundled into radial bins \(Q\) defined by lower and upper radial bounds. Once a cell center solid harmonic vector pair \({\bf R}(q)\) and \({\bf I}(q)\) for a particular cell has been calculated, its radial bin location \(q\rightarrow Q\) is determined and its contribution is added to the radial bin moments \({\bf M}^R(Q)\) and \({\bf M}^I(Q)\). The computational definition of the radial bin moments is

\[\begin{split}\begin{aligned} \label{Eqn:Moment computational definition} {\bf M}^R(Q) & = & \sum_{q\leq Q}{\bf R}(q)m(q) \\ {\bf M}^I(Q) & = & \sum_{q\geq Q}{\bf I}(q)m(q),\end{aligned}\end{split}\]

where \(q\leq Q\) means including all cells belonging to \(Q\) and all radial bins with lower radial boundaries than \(Q\). The two basic operations of the multipole solver are thus: i) assembly of the radial bin moments and ii) formation of the scalar products via Eq.([Eqn:Poisson discrete correct real]) to obtain the potentials. The memory declaration of the moment array should reflect the way the individual moment components are addressed and the most efficient layout puts the angular momentum indices in rows and the radial bin indices in columns.

How do we extract moments \({\bf M}^R({\bf x})\) and \({\bf M}^I({\bf x})\) at any particular position \({\bf x}\) inside the domain (and, in particular, at the cell face positions \({\bf x}_F\)), which are ultimately needed for the potential evaluation at that location? Assume that the location \({\bf x}\) corresponds to a particular radial bin \({\bf x}\rightarrow Q\). Consider the three consecutive radial bins \(Q-1\), \(Q\) and \(Q+1\), together with their calculated moments:

\[\begin{split}\begin{array}{r|r|r} {\bf M}^R(Q-1) & {\bf M}^R(Q) & {\bf M}^R(Q+1) \\ {\bf M}^I(Q-1) & {\bf M}^I(Q) & {\bf M}^I(Q+1) \end{array}\end{split}\]

Let us concentrate on the \(Q\) bin, whose lower and upper radial limits are shown as solid vertical lines. The radial distance corresponding to \({\bf x}\) splits the \(Q\) bin into two parts: the left fractional part, denoted \(R_{frac}\), and the right fractional part, denoted \(I_{frac}\). Since both \({\bf M}^R(Q-1)\) and \({\bf M}^I(Q+1)\) are completely contained respectively in \({\bf M}^R(Q)\) and \({\bf M}^I(Q)\), the moments at \({\bf x}\) be approximately evaluated as:

\[\begin{split}\begin{aligned} {\bf M}^R({\bf x}) & = & {\bf M}^R(Q-1) + R_{frac}\left[{\bf M}^R(Q)-{\bf M}^R(Q-1)\right] \label{Eqn:Cell moment computational definition 1} \\ {\bf M}^I({\bf x}) & = & {\bf M}^I(Q+1) + I_{frac}\left[{\bf M}^I(Q)-{\bf M}^I(Q+1)\right], \label{Eqn:Cell moment computational definition 2}\end{aligned}\end{split}\]

The extraction of the moments via ([Eqn:Cell moment computational definition 1]) and ([Eqn:Cell moment computational definition 2]) is of course an approximation that relies on the statistically dense distribution of the individual cell center moments inside each radial bin. For bins which are reasonably far away from the expansion center this statistical approximation is valid but for those close to the expansion center the statistical distribution does not hold and calculating the moments via the above scheme introduces a large statistical error. The way out of this problem is to move from a statistical radial bin description around the expansion center to a more discrete one, by constructing very narrow isolated radial bins. The code is thus forced to analyze the detailed structure of the geometrical domain grid surrounding the expansion center and to establish the inner radial zone of discrete distributed radial bins. The statistical radial bins are then referred to as belonging to the outer radial zone(s).

While the structure of the inner radial zone is fixed due to the underlying geometrical grid, the size of each radial bin in the outer radial zones has to be specified by the user. There is at the moment no automatic derivation of the optimum (accuracy vs memory cost) bin size for the outer zones. There are two types of radial bin sizes defined for the Flash-X multipole solver: i) exponentially and/or ii) logarthmically growing:

\[\begin{split}\begin{aligned} \mbox{exponential bin size upper radial limit} & = & s\cdot \Delta r \cdot Q^t \label{Eqn:Exponential bin definition} \\ \mbox{logarithmic bin size upper radial limit} & = & s\cdot \Delta r \cdot {e^{tQ}-1\over e^t-1}. \label{Eqn:Logarithmic bin definition}\end{aligned}\end{split}\]

In these definitions, \(\Delta r\) is a small distance ’atomic’ (basic unit) radial measure, defined as half the geometric mean of appropriate cell dimensions at highest refinement level, \(s\) is a scalar factor to optionally increase or decrase the atomic unit radial measure and \(Q = 1,2,\ldots\) is a local bin index counter for each outer zone. Note, that since \(\Delta r\) measures a basic radial unit along the radial distance from the expansion center (which, for approximate spherical problems, is located close to the domain’s geometrical origin), only those cell dimensions for calculating each \(\Delta r\) are taken, which are directly related to radial distances from the geometrical domain origin. For 3D cylindrical domain geometries for example, only the radial cylindrical and z-coordinate cell dimensions determine the 3D radial distance from the 3D cylindrical domain origin. The angular coordinate is not needed. Likewise for spherical domains only the radial cell coordinate is of importance. Definitions ([Eqn:Exponential bin definition]) and ([Eqn:Logarithmic bin definition]) define the upper limit of the radial bins. Hence in order to obtain the true bin size for the \(Q\)-th bin one has to subtract its upper radial limit from the corresponding one of the \((Q-1)\)-th bin:

\[\begin{split}\begin{aligned} \mbox{$Q$-th exponential bin size} & = & s\cdot \Delta r \cdot \left[Q^t-(Q-1)^t\right] \\ \mbox{$Q$-th logarithmic bin size} & = & s\cdot \Delta r \cdot e^{t(Q-1)}.\end{aligned}\end{split}\]

In principle the user can specify as many outer zone types as he/she likes, each having its own exponential or logarithmic parameter pair \(\{s,t\}\).

Multithreading of the code is currently enabled in two parts: 1) during moment evaluation and 2) during potential evaluation. The threading in the moment evaluation section is achieved by running multiple threads over separate, non-conflicting radial bin sections. Moment evaluation is thus organized as a single loop over all relevant radial bins on each processor. Threading over the potential evaluation is done over blocks, as these will address different non-conflicting areas of the solution vector.

The improved multipole solver was extensively tested and several runs have been performed using large domains (\(>10^{10}\)) and extremely high angular numbers up to \(L=100\) for a variety of domain geometries. Currently, the following geometries can be handled: 3D cartesian, 3D cylindrical, 2D cylindrical, 2D spherical and 1D spherical. The structure of the code is such that addition of new geometries, should they ever be needed by some applications, can be done rapidly.

Multigrid

The Grid/GridSolvers/Multigrid module is appropriate for general source distributions. It solves Poisson’s equation for 1, 2, and 3 dimensional problems with Cartesian geometries. It only supports the AMReX Grid in the current version (See AMReX documentation for more detail). It may be included by setup or Config by including:

physics/Gravity/GravityMain/Poisson/Multigrid

The multigrid solver may also be included stand-alone using:

Grid/GridSolvers/Multigrid

HYPRE

As a part of implicit time advancement we end up with a system of equations that needs to be solved at every time step. In Flash-X the HYPRE linear algebra package is used to solve these systems of equations. Therefore it is necessary to install Hypre if this capability of Flash-X is to be used.

Grid_advanceDiffusion is the API function which solves the system of equations. This API is provided by both the split and unsplit solvers. The unsplit solver uses HYPRE to solve the system of equations and split solver does a direct inverse using Thomas algorithm. Note that the split solver relies heavily on PFFT infrastructure for data exchange and a significant portion of work in split Grid_advanceDiffusion involves PFFT routines. In the unsplit solver the data exchange is implicitly done within HYPRE and is hidden.

The steps in unsplit Grid_advanceDiffusion are as follows:

• Setup HYPRE grid object

• Exchange Factor B

• Set initial guess

• Compute HYPRE Matrix M such that B = MX

• Compute RHS Vector B

• Compute matrix A

• Solve system AX = B

• Update solution (in Flash-X)

Mapping UG grid to HYPRE matrix is trivial, however mapping AMR grid to a HYPRE matrix can be quite complicated. The process is simplified using the grid interfaces provided by HYPRE.

• Struct Grid interface

• SStruct Grid interface

• IJ System interface

Setting up the HYPRE grid object is one of the most important step of the solution process. We use the SSTRUCT interface provided in HYPRE to setup the grid object. Since the HYPRE Grid object is mapped directly with Flash-X grid, whenever the Flash-X grid changes the HYPRE grid object needs to be updated. Consequentlywith AMR the HYPRE grid setup might happen multiple times.

Setting up a HYPRE grid object is a two step process,

• Creating stenciled relationships.

• Creating Graph relationships.

Stenciled relationships typically exist between leaf blocks at same refinement level (intra part) and graph relationships exist between leaf blocks at different refinement levels (inter part). The fine-coarse boundary is handled in such a way that fluxes are conserved at the interface (see for details). UG does not require any graph relationships.

Whether a block needs a graph relationship depends on the refinement level of it’s neighbor. While this information is not directly available in PARAMESH, it is possible to determine whether the block neighbor is coarser or finer. Combining this information with the constraint of at best a factor of two jump in refinement at block boundaries, it is possible to compute the part number of a neighbor block, which in turn determines whether we need a graph. Creating a graph involves creating a link between all the cells on the block boundary.

Once the grid object is created, the matrix and vector objects are built on the grid object. The diffusion solve needs uninterpolated data from neighbor blocks even when there is a fine-coarse boundary, therefore it cannot rely upon the guardcell fill process. A two step process is used to handle this situation,

• Since HYPRE has access to X(at n, i.e., initial guess), the RHS vector B can be computed as MX where M is a modified Matrix.

• Similarly the value of Factor B can be shared across the fine-coarse boundary by using Grid_conserveFluxes,the fluxes need to be set in a intuitive to way to achieve the desired effect.

With the computation of Vector B (RHS), the system can be solved using HYPRE and UNK can be updated.

Grid Geometry

Flash-X can use various kinds of coordinates (“geometries”) for modeling physical problems. The available geometries represent different (orthogonal) curvilinear coordinate systems.

The geometry for a particular problem is set at runtime (after an appropriate invocation of setup) through the geometry runtime parameter, which can take a value of “cartesian”, “spherical”, “cylindrical”, or “polar”. Together with the dimensionality of the problem, this serves to completely define the nature of the problem’s coordinate axes (). Note that not all Grid implementations support all geometry/dimension combinations. Physics units may also be limited in the geometries supported, some may only work for Cartesian coordinates.

The core code of a Grid implementation is not concerned with the mapping of cell indices to physical coordinates; this is not required for under-the-hood Grid operations such as keeping track of which blocks are neighbors of which other blocks, which cells need to be filled with data from other blocks, and so on. Thus the physical domain can be logically modeled as a rectangular mesh of cells, even in curvilinear coordinates.

There are, however, some areas where geometry needs to be taken into consideration. The correct implementation of a given geometry requires that gradients and divergences have the appropriate area factors and that the volume of a cell is computed properly for that geometry. Initialization of the grid as well as AMR operations (such as restriction, prolongation, and flux-averaging) must respect the geometry also. Furthermore, the hydrodynamic methods in Flash-X are finite-volume methods, so the interpolation must also be conservative in the given geometry. The default mesh refinement criteria of Flash-X also currently take geometry into account, see above.

Understanding 1D, 2D, and Curvilinear Coordinates

In the context of Flash-X, curvilinear coordinates are most useful with 1-d or 2-d simulations, and this is how they are commonly used. But what does it mean to apply curvilinear coordinates in this way? And what does it mean to do a 1D or a 2D simulation of threedimensional reality? Physical reality has three spatial dimensions (as far as the physical problems simulated with Flash-X are concerned). In Cartesian coordinates, it is relatively straightforward to understand what a 2-d (or 1-d) simulation means: “Just leave out one (or two) coordinates.” This is less obvious for other coordinate systems, therefore some fundamental discussion follows.

A reduced dimensionality (RD) simulation can be naively understood as taking a cut (or, for 1-d, a linear probe) through the real 3-d problem. However, there is also an assumption, not always explicitly stated, that is implied in this kind of simulation: namely, that the cut (or line) is representative of the 3-d problem. This can be given a stricter meaning: it is assumed that the physics of the problem do not depend on the omitted dimension (or dimensions). A RD simulation can be a good description of a physical system only to the degree that this assumption is warranted. Depending on the nature of the simulated physical system, non-dependence on the omitted dimensions may mean the absence of force and/or momenta vector components in directions of the omitted coordinate axes, zero net mass and energy flow out of the plane spanned by the included coordinates, or similar.

For omitted dimensions that are lengths — \(z\) and possibly \(y\) in Cartesian, and \(z\) in cylindrical and polar RD simulations — one may think of a 2-d cut as representing a (possibly very thin) layer in 3-d space sandwiched between two parallel planes. There is no a priori definition of the thickness of the layer, so it is not determined what 3-d volume should be asigned to a 2-d cell in such coordinates. We can thus arbitrarily assign the length “\(1\)” to the edge length of a 3-d cell volume, making the volume equal to the 2-d area. We can understand generalizations of “volume” to 1-d, and of “face areas” to 2-d and 1-d RD simulations with omitted linear coordinates, in an equivalent way: just set the length of cell edges along omitted dimensions to 1.

For omitted dimensions that are angles — the \(\theta\) and \(\phi\) coordinates on spherical, cylindrical, and polar geometries — it is easier to think of omitting an angle as the equivalent of integrating over the full range of that angle coordinate (under the assumption that all physical solution variables are independent of that angle). Thus omitting an angle \(\phi\) in these geometries implies the assumption of axial symmetry, and this is noted in . Similarly, omitting both \(\phi\) and \(\theta\) in spherical coordinates implies an assumption of complete spherical symmetry. When \(\phi\) is omitted, a 2-d cell actually represents the 3-d object that is generated by rotating the 2-d area around a \(z\)-axis. Similarly, when only \(r\) is included, 1-d cells (i.e., \(r\) intervals) represent hollow spheres or cylinders. (If the coordinate interval begins at \(r_l=0.0\), the sphere or cylinder is massive instead of hollow.)

As a result of these considerations, the measures for cell (and block) volumes and face areas in a simulation depends on the chosen geometry. Formulas for the volume of a cell dependent on the geometry are given in the geometry-specific sections further below.

As discussed in , to ensure conservation at a jump in refinement in AMR grids, a flux correction step is taken. The fluxes leaving the fine cells adjacent to a coarse cell are used to determine more accurately the flux entering the coarse cell. This step takes the coordinate geometry into account in order to accurately determine the areas of the cell faces where fine and coarse cells touch. By way of example, an illustration is provided below in the section on cylindrical geometry.

Extensive Quantities in Reduced Dimensionality

The considerations above lead to some consequences for the understanding of extensive quantities, like mass or energies, that may not be obvious.

The following discussion applies to geometries with omitted dimensions that are lengths — \(z\) and possibly \(y\) in Cartesian, and \(z\) in cylindrical and polar RD simulations. We will consider Cartesian geometries as the most common case, and just note that the remaining cases can be thought of analogously.

In 2D Cartesian, the “volume” of a cell should be \(\Delta V = \Delta x\,\Delta y\). We would like to preserve the form of equations that relate extensive quantities to their densities, e.g., \(\Delta m = \rho \Delta V\) for mass and \(\Delta E_{\mathrm tot} = \rho e_{\mathrm tot}\Delta V\) for total energy in a cell. We also like to retain the usual definitions for intensive quantities such as density \(\rho\), including their physical values and units, so that material density \(\rho\) is expressed in \(g/cm^3\) (more generally \(M/L^3\)), no matter whether 1D, 2D, or 3D. We cannot satisfy both desiderata without modifying the interpretation of “mass”, “energy”, and similar extensive quantities in the system of equations modeled by Flash-X.

Specifically, in a 2D Cartesian simulation, we have to interpret “mass” as really representing a linear mass density, measured in \(M/L\). Similarly, an “energy” is really a linear energy density, etc.

In a 1D Cartesian simulation, we have to interpret “mass” as really representing a surface mass density, measured in \(M/L^2\), and an “energy” is really a surface energy density.

(There is a different point of view, which amounts to the same thing: One can think of the “mass” of a cell (in 2D) as the physical mass contained in a threedimensional cell of volume \(\Delta x \Delta y \Delta z\) where the cell height \(\Delta z\) is set to be exactly 1 length unit. Always with the understanding that “nothing happens” in the \(z\) direction.)

Note that this interpretation of “mass”,“energy”, etc. must be taken into account not just when examining the physics in individual cells, but equally applies for quantities integrated over larger regions, including the “total mass” or “total energy” etc. reported by Flash-X in flash.dat files — they are to be interpreted as (linear or surface) densities of the nominal quantities (or, alternatively, as integrals over 1 length unit in the missing Cartesian directions).

Choosing a Geometry

The user chooses a geometry by setting the geometry runtime parameter in flash.par. The default is cartesian (unless overridden in a simulation’s Config file). Depending on the Grid implementation used and the way it is configured, the geometry may also have to be compiled into the program executable and thus may have to be specified at configuration time; the setup flag -geometry should be used for this purpose, see .

The geometry runtime parameter is most useful in cases where the geometry does not have to be specified at compile-time, in particular for the Uniform Grid. The runtime parameter will, however, always be considered at run-time during Grid initialization. If the geometry runtime parameter is inconsistent with a geometry specified at setup time, Flash-X will then either override the geometry specified at setup time (with a warning) if that is possible, or it will abort.

This runtime parameter is used by the Grid unit and also by hydrodynamics solvers, which add the necessary geometrical factors to the divergence terms. Next we describe how user code can use the runtime parameter’s value.

Getting Geometry Information in Program Code

The Grid unit provides an accessor Grid_getGeometry property that returns the geometry as an integer, which can be compared to the symbols {CARTESIAN, SPHERICAL, CYLINDRICAL, POLAR} defined in “constants.h” to determine which of the supported geometries we are using. A unit writer can therefore determine flow-control based on the geometry type (see ). Furthermore, this provides a mechanism for a unit to determine at runtime whether it supports the current geometry, and if not, to abort.

#include “constants.h”

integer :: geometry

call Grid_getGeometry(geometry)

select case (geometry)

case (CARTESIAN)

! do Cartesian stuff here …

case (SPHERICAL)

! do spherical stuff here …

case (CYLINDRICAL)

! do cylindrical stuff here …

case (POLAR)

! do polar stuff here …

end select

Coordinate information for the mesh can be determined via the Grid_getCellCoords routine. This routine can provide the coordinates of cells at the left edge, right edge, or center. The width of cells can be determined via the Grid_getDeltas routine. Angle values and differences are given in radians. Coordinate information for a block of cells as a whole is available through Grid_getBlkCenterCoords and Grid_getBlkPhysicalSize.

Note the following difference between the two groups of routines mentioned in the previous two paragraphs: the routines for volumes and areas take the chosen geometry into account in order to return geometric measures of physical volumes and faces (or their RD equivalents). On the other hand, the routines for coordinate values and widths return values for \(X\), \(Y\), and \(Z\) directly, without converting angles to (arc) lengths.

Available Geometries

Currently, all of Flash-X’s physics support one-, two-, and (with a few exceptions explicitly stated in the appropriate chapters) three-dimensional Cartesian grids. Some units, including the Flash-X Grid unit and PPM hydrodynamics unit (), support additional geometries, such as two-dimensional cylindrical (\(r,z\)) grids, one/two-dimensional spherical (\(r\))/(\(r, \theta\)) grids, and two-dimensional polar (\(r, \phi\)) grids. Some specific considerations for each geometry follow.

The following tables use the convention that \(r_l\) and \(r_r\) stand for the values of the \(r\) coordinate at the “left” and “right” end of the cell’s \(r\)-coordinate range, respectively (i.e., \(r_l < r_r\) is always true), and \(\Delta r = r_r-r_l\); and similar for the other coordinates.

Cartesian geometry

Flash-X uses Cartesian (plane-parallel) geometry by default. This is equivalent to specifying

geometry = “cartesian”

in the runtime parameter file.

Cell Volume in Cartesian Coordinates

1-d	\(\Delta x\)
2-d	\(\Delta x \Delta y\)
3-d	\(\Delta x \Delta y \Delta z\)

Cylindrical geometry

To run Flash-X with cylindrical coordinates, the geometry parameter must be set thus:

geometry = “cylindrical”

Cell Volume in Cylindrical Coordinates

1-d	\(\pi (r_r^2 - r_l^2)\)
2-d	\(\pi (r_r^2 - r_l^2) \Delta z\)
3-d	\(\frac{1}{2} (r_r^2 - r_l^2) \Delta z \Delta \phi\)

As in other non-Cartesian geometries, if the minimum radius is chosen to be zero (xmin = 0.), the left-hand boundary type should be reflecting (or axisymmetric). Of all supported non-Cartesian geometries, the cylindrical is in 2-d most similar to a 2-d coordinate system: it uses two linear coordinate axes (\(r\) and \(z\)) that form a rectangular grid physically as well as logically.

As an illustrative example of the kinds of considerations necessary in curved coordinates, shows a jump in refinement along the cylindrical ‘\(z\)’ direction. When performing the flux correction step at a jump in refinement, we must take into account the area of the annulus through which each flux passes to do the proper weighting. We define the cross-sectional area through which the \(z\)-flux passes as

\[A = \pi (r_r^2 - r_l^2) \enskip .\]

The flux entering the coarse cell above the jump in refinement is corrected to agree with the fluxes leaving the fine cells that border it. This correction is weighted according to the areas

\[f_3 = \frac{A_1 f_1 + A_2 f_2}{A_3}~.\]

For fluxes in the radial direction, the cross-sectional area is independent of the height, \(z\), so the corrected flux is simply taken as the average of the flux densities in the adjacent finer cells.

Spherical geometry

One or two dimensional spherical problems can be performed by specifying

geometry = “spherical”

in the runtime parameter file.

Cell Volume in Spherical Coordinates

1-d	\(\frac{4}{3} \pi (r_r^3 - r_l^3)\)
2-d	\(\frac {2}{3} \pi (r_r^3 - r_l^3) (\cos(\theta_l) - \cos(\theta_r))\)
3-d	:math:` frac{1}{3} (r_r^3 - r_l^3) (cos(theta_l) - cos(theta_r)) Delta phi`

If the minimum radius is chosen to be zero (xmin = 0.), the left-hand boundary type should be reflecting.

Polar geometry

Polar geometry is a 2-D subset of 3-D cylindrical configuration without the “z” coordinate. Such geometry is natural for studying objects like accretion disks. This geometry can be selected by specifying

geometry = “polar”

in the runtime parameter file.

Cell Volume in Polar Coordinates

1-d	\(\pi (r_r^2 - r_l^2)\)
2-d	\(\frac{1}{2} (r_r^2 - r_l^2)\Delta \phi\)
3-d	\(\frac{1}{2} (r_r^2 - r_l^2)\Delta \phi \Delta z\) (not supported)

As in other non-Cartesian geometries, if the minimum radius is chosen to be zero (xmin = 0.), the left-hand boundary type should be reflecting.