Macroprocessor

With the advent of accelerators we need to have many more alternative implementations to accommodate differences in hardware characteristics. Combined with the already existing alternatives, in many situations we would have had a combinatorial explosion of maintained alternatives to continue to have the same level of flexibility in application configurability on different platforms. Often, the alternatives for different devices need either a different data layout or a different control flow while the arithmetic of the algorithm remains the same. Hence, without some form of unification of the code base there would be rampant duplication of arithmetic code leading to maintenance difficulties. This is the primary challenge that C++ based tools addresses through template meta-programming, which is not available in C or Fortran. Another obvious solution is to use macros to encode the invariant arithmetic code. We have taken this approach, but instead of using pre-processor macros, we built a more capable and versatile macroprocessor described below.

Using Macros

A function in a physics unit typically has some arithmetic interspersed with some control flow logic. Often the features of the implementation that need to be modified for optimization are data layouts and control flow without changing the arithmetic. We begin by casting a non-trivial function in the physics unit of the code as a collection of code blocks. Some code blocks may be declarations, some may implement the control logic, and some will implement the numerics of the function. Sometimes arithmetic and logic blocks cannot be separated out so some code blocks have both. These code blocks become components in a hierarchical composability through the use of macros in the form of key-value dictionary where values are code snippets of arbitrary length and complexity. Keys, or macros are user-defined with a provision for multiple alternative definitions, including null definitions, which lets them mimic specializations similar to those provided by C++ template meta-programming.

The macros supported in Flash-X are similar to C preprocessor macros in how they are defined. They permit arguments, are allowed to be inlined in a regular programming language statement, and one macro name can be embedded in another macro’s definition as long as self-reference is avoided. Where are tool differs from the preprocessor is in permitting alternative definitions, including null definitions for macros, and an arbitration mechanism to select a specific definition. The macroprocessor is written in python and the definitions are stored in ``.ini’’ files, according to the Python ConfigParser format. The source files needing translation are given the extension ``.F90-mc’’ to differentiate them from the source files that do not need expansion.

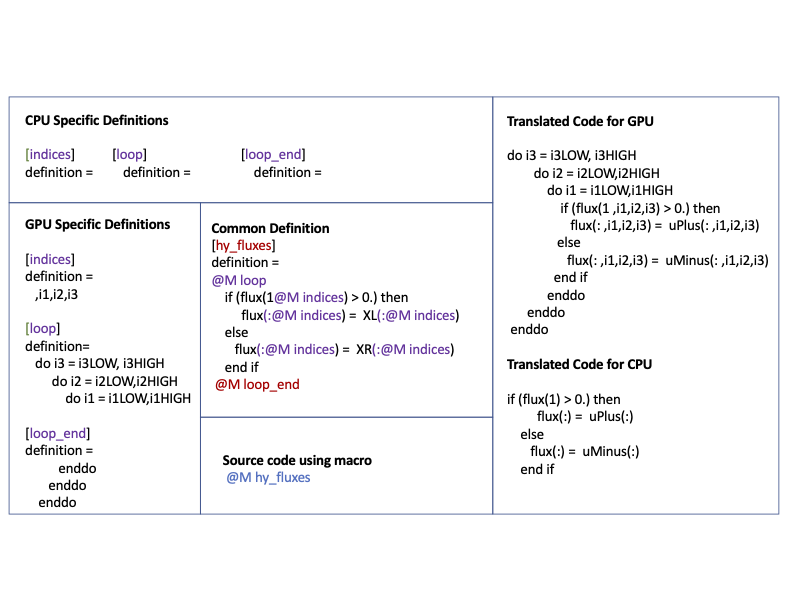
Provision for alternative definitions combined with the ability to embed a macro anywhere in the code permits arbitrary granularity in code variants. The example shown below exhibits use of macros at various granularities. In this example the CPU version of the code uses 1D scratch arrays operating on one spatial data point at a time, while the GPU version uses 4D scratch arrays operating on all spatial data points simultaneously. Both versions otherwise have identical logic for copying data into the target scratches. The macro indices is the finest grain macro, with its null definition for the CPU version allows unification of the scratch space reference in the code. Similarly, macros loop and loop_end have null definitions for the CPU version. Also, hy_flux is itself a macro which has other other macros embedded in it. This approach can be particularly useful when the involved arithmetic is complex but identical in both versions and the only difference is in the data layout and access patterns.

An additional feature is required if more than one variant needs to be included in an application instance. It must be possible to invoke each variant under different identifiers. For example, if a function foo can generate two variants, var1 and var2, both of which need to be included in the application, then it must be possible to call them as foo_var1 and foo_var2, but if they are exclusive in another application instance then it should be possible to simply call foo. Furthermore, with multiple alternative definitions existing for macros, a mechanism is needed to arbitrate on which variants are to be built with which definitions. The setup tool of Flash-X already had arbitration built-in upto the granularity of file. For macros arbitration is needed upto the level of a single macro definition. The setup tool is enhance to keep track of macro definitions in addition to files that it has encountered. The inheritance rules remain the same as those for files, a local level directory inherits all definitions and replaces those that are present it any of its own “.ini” files. As with files, the definitions placed in the Simulation directory of the application override all definitions encountered earlier.

We have defined several macros for convenience that are available in the file “macro_processors.ini” in the bin directory. The more commonly used ones are described below.

[loop_3d]

args=limits

definition =

do k=limits(LOW,KAXIS),limits(HIGH,KAXIS)

do j=limits(LOW,JAXIS),limits(HIGH,JAXIS)

do i=limits(LOW,IAXIS),limits(HIGH,IAXIS)

Use as @M loop_3d(blkLimits) results in the loop bounds for a triply nested loop in place of the macro name where every occurence of “limits” is replaced with “blkLimits”

[bounds_3d]

args=limits

definition =

limits(LOW,IAXIS):limits(HIGH,IAXIS),&

limits(LOW,JAXIS):limits(HIGH,JAXIS),&

limits(LOW,KAXIS):limits(HIGH,KAXIS)

usage in declaration as

real, dimension(@M bounds_3d(blkLimits)) :: arr

will result in a 3D array being declared with bounds defined using the supplied two dimensional array blkLimits.

[bounds_2d]

args=x1,x2,limits

definition =

limits(LOW,x1AXIS):limits(HIGH,x1AXIS),&

limits(LOW,x2AXIS):limits(HIGH,x2AXIS)

This macros is used for declaring 2D arrays when bounds are included in the supplied array to replace limits. This one has an additional feature, x1 and x2 can be “I”, “J”, or “K” to define which two directions are included in the array

[tileDesc_get]

args =lim1,lim2,lim3,del

definition =

lim1(:,:)=tileDesc%%limits

lim2(:,:)=tileDesc%%blkLimitsGC

lim3(:,:)=tileDesc%%grownLimits

call tileDesc%%deltas(del)

level=tileDesc%%level

@M tileDesc_get(blkLimits,blkLimitsGC,grownLimits,deltas) fills the supplied arrays with the corresponding tile data. It assumes that all these variables have been declared in the code. The argument lim1 has bounds for the interior cells of the block where the solution is to be advanced and lim2 has bounds for all cells of the block including the guardcells. The third argument lim3 is needed for tiling, that is if a block is subdivided into tiles, the lim3 has bounds for the section of the block that is the part of the tile and also includes those interior cells that effectively become the guardcells for the cells that are to be advanced in this tile. The final argument is a real 1D array of size 3 in which deltax, deltay and delaz are returned. Note that the function returns valid values for 1:NDIM dimensions only. Also note that this macro fetches the value of the “level” assuming that it has been declared as is in the declaration section of the code. For convenience one can use the next macro, “tileDesc_declare” in the declaration section of the code to ensure that the variables are appropriately declared. Note that the first three arguments given to the two macros must be identical and identically ordered for correct behavior.

[tileDesc_declare]

args = lim1,lim2,lim3

definition =

integer :: level

integer, dimension(LOW:HIGH,MDIM) :: lim1,lim2,lim3

real,dimension(MDIM) :: deltas

There are additional tile related macros that can be put in the “use” and declaration sections of the code, as well as used as arguments. It is not necessary to use any of these macros, however, users are strongly encouraged to use them wherever needed. If we need to change the tile class for any reason, it would be straightforward to make the code compatible everywhere by just making the change to the macro definition instead of writing scripts to do search and replace.

The next few macros pertain to the use of iterators in the code. As with tiles there is one for the “use” section and one for the “declare” section. For starting the iterator two different macros are provided; one compatible with AMReX’s prefered mode of operating on a level by level basis, and the other one compatible with Paramesh’s preference of operating on all levels in the same loop. The arguments for the two

[iter_all_begin]

args=x1,t1,lim1,lim2,del

definition =

call Grid_getTileIterator(itor, x1, tiling=t1)

do while(itor%%isValid())

call itor%%currentTile(tileDesc)

@M tileDesc_get(lim1,lim2,grownLimits,del)

call tileDesc%%getDataPtr(Uin, CENTER)

This is the macro for Paramesh preferred iterators where x1 is the argument for the blocktype (usually LEAF} and t1 is either .true. if tiing is desired, and .false. if it is not. The arguments lim1 and lim2 are the usual blkLimits and blkLimitsGC. Note that the macros is assuming that grownLimits and Uin are declared as expected, they are not among the arguments. The next macro has an additional argument l1, where the value of level resides.

[iter_level_begin]

args=x1,t1,l1,lim1,lim2,del

definition=

call Grid_getTileIterator(itor,x1,level=l1,tiling=t1)

do while(itor%%isValid())

call itor%%currentTile(tileDesc)

@M tileDesc_get(lim1,lim2,grownLimits,del)

call tileDesc%%getDataPtr(Uin, CENTER)

The next macro is to be used at the end of the iterator loop. It release the pointer Uin, and also the tile iterator.

[iter_end]

definition =

call tileDesc%%releaseDataPtr(Uin,CENTER)

call itor%%next()

end do !!block loop

call Grid_releaseTileIterator(itor)